The Many Different Ways To Make Money With DeFi

Last week, we went through the details of what’s driving the resurgence of interest in DeFi from a technical perspective.

This week, we’ll cover the many exciting ways we can look to make money in the DeFi space — many of which we’ve not yet covered before, so buckle up!

First thing: this is purely explanatory and is in no way meant to suggest you do something with your money. Your money, your choices, your risk.

Second, you’ll need some tools:

Tools you need

Required:

A web3 enabled browser (I like Brave) and / or  a web3 enabled wallet:

MetaMask (desktop)

Argent (mobile)

Coinbase Wallet (mobile)

Exchange account to onboard fiat to crypto (use https://www.buybitcoinworldwide.com/ to see what works best in your country)

Hardware wallet for cold storage (I like Ledger)

Now, let’s get down to business.

Protocols & Applications

This week we’ll be covering each of these:

Aave

Argent

Augur

Balancer

Rebalance stablecoins with Balancer

If you have some ETH or ERC20 tokens lying around you’ve probably already asked the question: how should I put these to work? With DeFi there are a multitude for you to earn money with your idle assets: from lending money to Compound, opening a Maker vault, to being a Uniswap liquidity provider.

Now there’s Balancer—a new option for providing liquidity. Balancer allows pools with different combinations of tokens (think token ETFs or index funds). With Balancer, any liquidity provider can customize their exposure while earning trading fees from the protocol.

What is Balancer?

Balancer is an AMM protocol that allows anyone to provide liquidity to existing Balancer pools or create one themselves. Each Balancer pool is composed of 2 to 8 tokens. Each of the tokens makes up a percentage of the total pool value: these are the token weights that are chosen at the moment of pool creation. The mathematical properties of Balancer protocol ensure that the value percentage of each token in a pool will stick closely to the weight even as the market prices of the tokens themselves vary.

A Balancer Pool is a self-balancing index fund

This means that each Balancer pool is a self-balancing index fund itself. But it gets better. In a conventional index fund the investor has to pay a fee for the rebalancing service, but in a Balancer pool the liquidity provider is actually rewarded for their service of providing liquidity to the protocol. They earn fees while their index funds are continuously rebalanced for them.

Why Balancer is a magical money lego

Balancer pools can be one of two kinds:

1. 1. 1. shared (i.e. finalized)
      2. private (i.e. controlled)

Shared pools have fixed parameters (they cannot be changed even by the pool creator) so that anyone can add liquidity to them. This is necessary since the pool creator could indirectly steal money from other liquidity providers in their pool if they could, for example by adding a new token they control all the supply of.

Private pools are as flexible as it gets: tokens can be removed/added, weights can be changed and even the swap fee can be adjusted. However, the only address that can provide liquidity to it is the pool creator. This is great for big index funds that manage funds of third parties for example.

But private pools get really interesting with smart pools.

Smart pools are private pools that are owned by smart contracts. These smart contracts can be used as a gateway for external users to add liquidity to pools under known conditions. Some great examples are:

• • PieDAO BTC++: the BTC++ pool is currently comprised of 4 different types of ERC-20 BTC synthetics. Through governance, PieDAO can change the weights of each of these types of tokenized BTC, add new types in the futures and even pause trading if one of the tokens has problems and loses its peg.
• • Bootstrapping liquidity pools: projects that are seeking to both make their native token liquid and also distribute tokens in a sale can use the concept of a smart pool that gradually flips the weights of its underlying tokens. This is an effective way of killing two birds with a stone: provide liquidity for your token at the same time as you exchange it for ETH or DAI to fund your project development.
• • RealT index fund: instead of having fragmented liquidity in many Uniswap Pools, RealT tokenized properties can all live in the same Balancer pool, effectively creating a RealT index fund. By using a smart pool, RealT can keep the possibility of adding new properties in the future, as well as changing the weights of existing ones (say for example one of them is refurbished and doubles in market value).

Compound

Curve

dYdX

Gnosis

InstaDapp

MCDEX

                Trade ETH perpetual on MCDEX

                What is MCDEX?

MCDEX is a decentralized trading platform for perpetual swaps and futures on Ethereum. The mission is to make investing in DeFi more accessible by providing financial services for users with different risk appetites.

Currently, the ETH perpetual contract is live on main net using an on-chain AMM and off-chain order book hybrid model.

With MCDEX, traders can long and short ETH with up to 10x leverage without taking custody of other assets, only ETH.

Liquidity Mining & MCB

In a nutshell, users can get MCB, MCDEX’s native token, by providing liquidity to the AMM pool.

The MCB token will allow key stakeholders of the MCDEX platform, i.e takers, liquidity providers, contributors of trading strategies, DeFi developers, etc, to participate in the governance to achieve sustainable and robust development.

Review of Perpetual Markets

A perpetual contract is a futures-like product but without an expiration date.

Since its inception, perpetuals have become one of the most popular instruments for crypto trading. Its trading price is anchored to the underlying asset price index through a funding payment mechanism (called the funding rate).

The funding payment balances out between long and short positions by charging between them. While CeFi platforms hold customer deposits and control the overall functioning of the platforms, DeFi platforms like MCDEX are non-custodial.

This is the primary reason why trading a perpetual contract on a decentralized exchange is far more beneficial than trading on a centralized exchange such as BitMEX. The fact that decentralized exchanges have no control over your funds, it’s much safer to trade on decentralized exchanges.

While MCDEX, dYdX, and FutureSwap offer similar products, each DEX has taken a different design approach with both their contract specifications and infrastructure.

Here’s a concise overview of each exchange and their respective perpetual swap products:

mStable

Opyn

                Make money selling ETH options with Opyn

                Selling Put Options

By selling a put option on ETH, you are selling someone the “right but not the obligation to sell you ETH at a pre-specified price”.

If the price of ETH remains above the strike price, then the seller of the option keeps the premium they earned for selling the option and is able to withdraw their USDC upon the option expiring.

If the price of ETH falls below the strike price, then the seller of the option may be obligated to buy ETH at the strike price (which could be higher than the market price of ETH). The image below demonstrates the payoff for a seller of a $200 Strike Put option on ETH.

How to use Opyn to provide ETH protection to other users

Requirements: The following section only works on a desktop browser. You will need your computer and MetaMask for the following to work.

You will also need some USDC and ETH (for gas) in your wallet.

Note: Gas is very expensive these days. In order to make a positive ROI by selling ETH options on Opyn, you’ll need a fair amount of capital to get started. I’m recommending at least $500+.

1.Go to https://opyn.co/#/sell

2.Connect your wallet by clicking the “Connect Wallet Button” on the top right corner.

3.Scroll down to the “Sell Protective Put Options on ETH Section”.

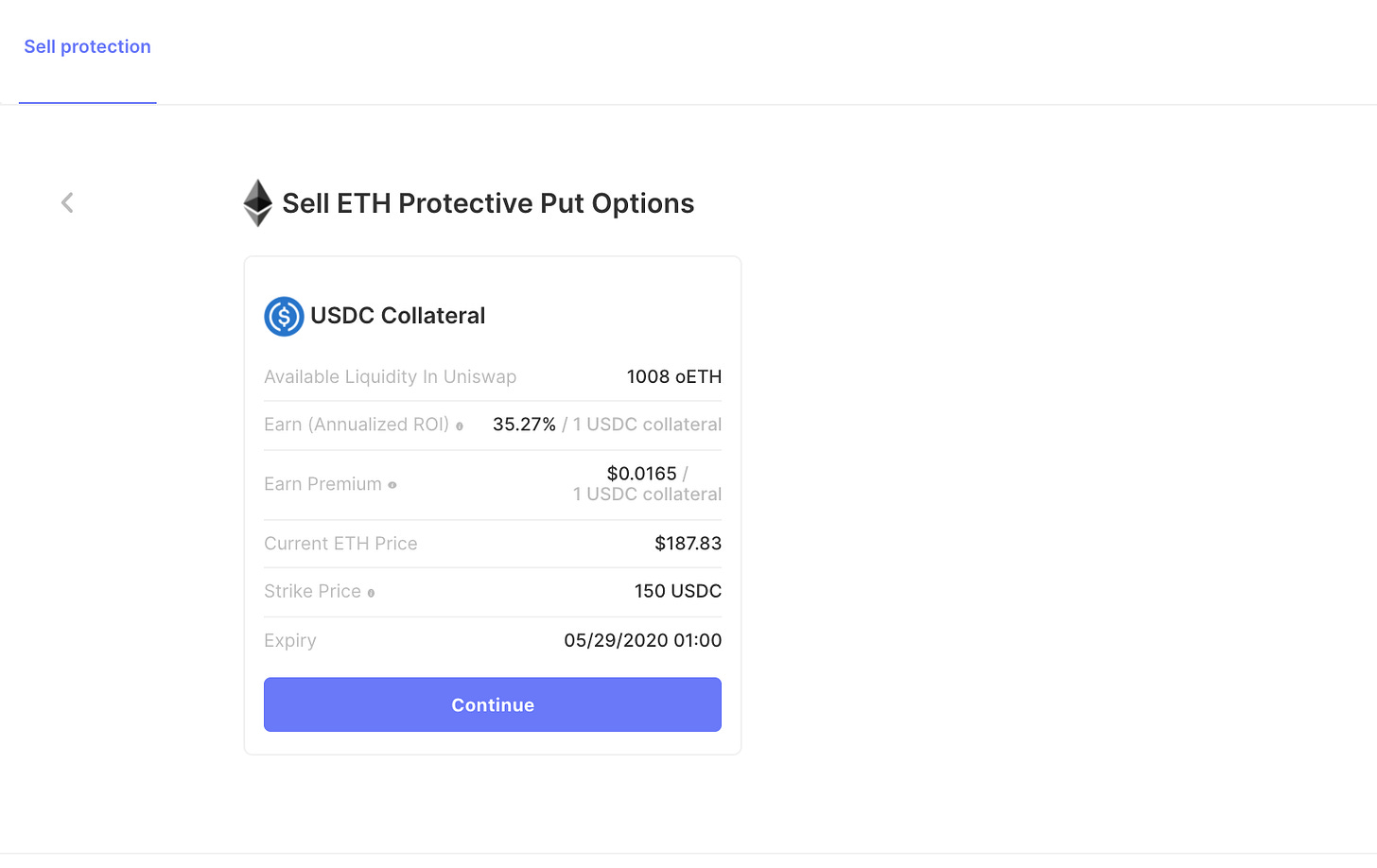
The expiry is the date that your protection will expire on. You are providing protection until that date.

Strike Price is the pre-specified price that you are agreeing to buy ETH at if ETH falls in price. You are effectively selling someone “the right but not the obligation to sell you their ETH at that price (the strike price)”.

The earned premium is how much you could make upfront per 1 USDC that you lock up as collateral.

The Annualized ROI is what your returns over the course of a year could look like if you continued to earn the current rate of premiums.

Choose the parameters that work best for you and click on that specific row.

4.You should see the page below. Click on the continue button if the strike price, expiry, earn premium all look good to you.

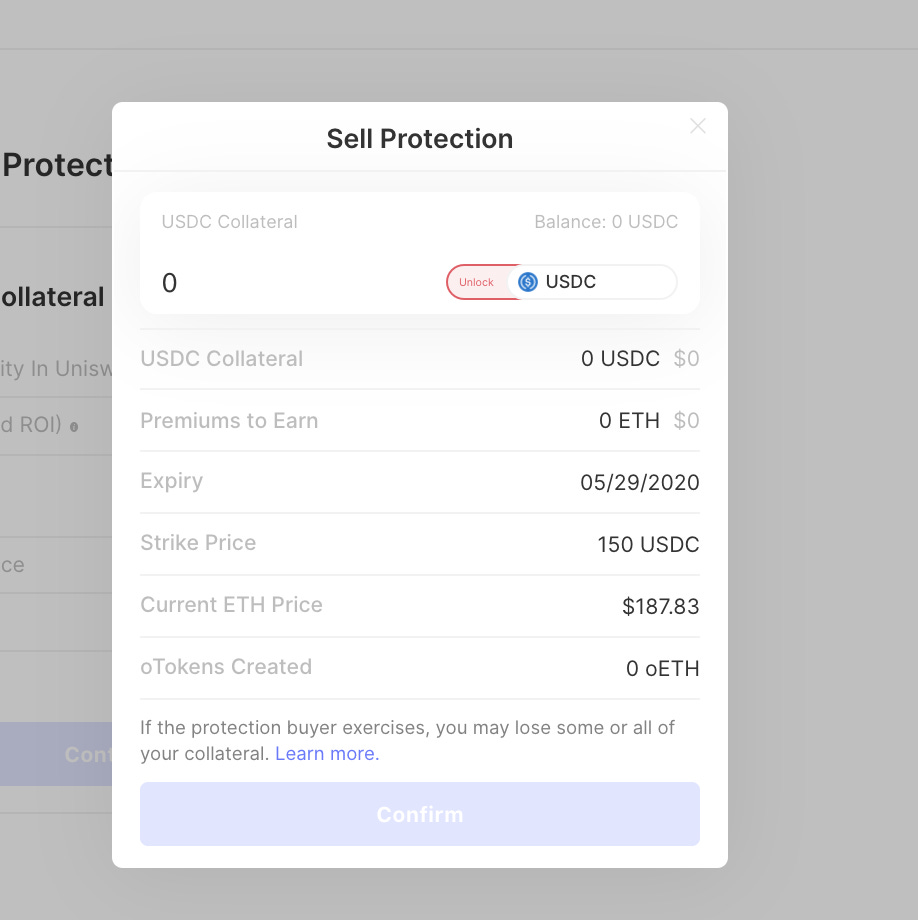
5.Unlock the modal that you see below to allow the contract to spend your USDC.

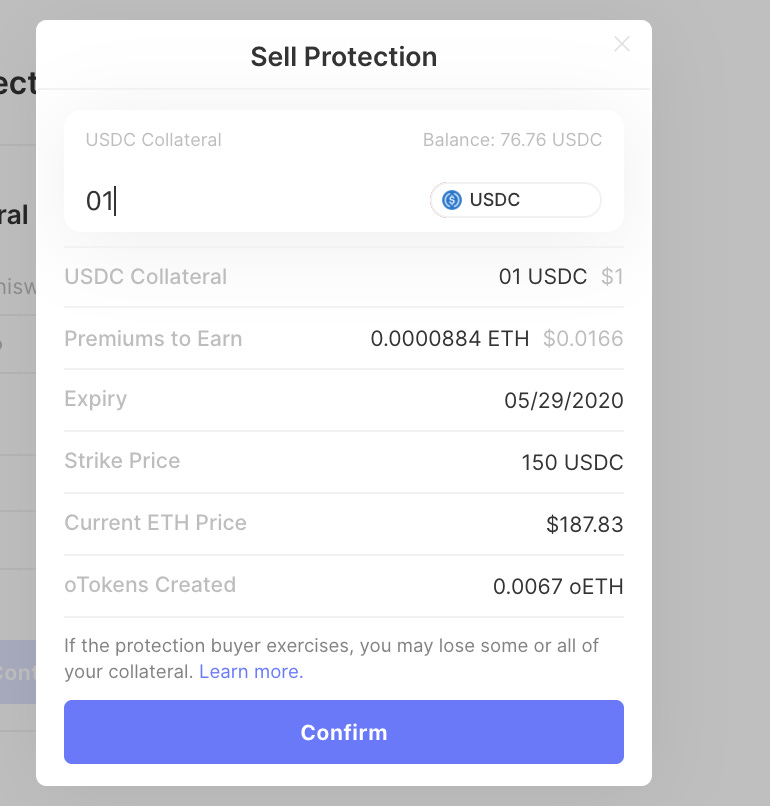
6.Enter the amount of USDC that you want to put down as collateral

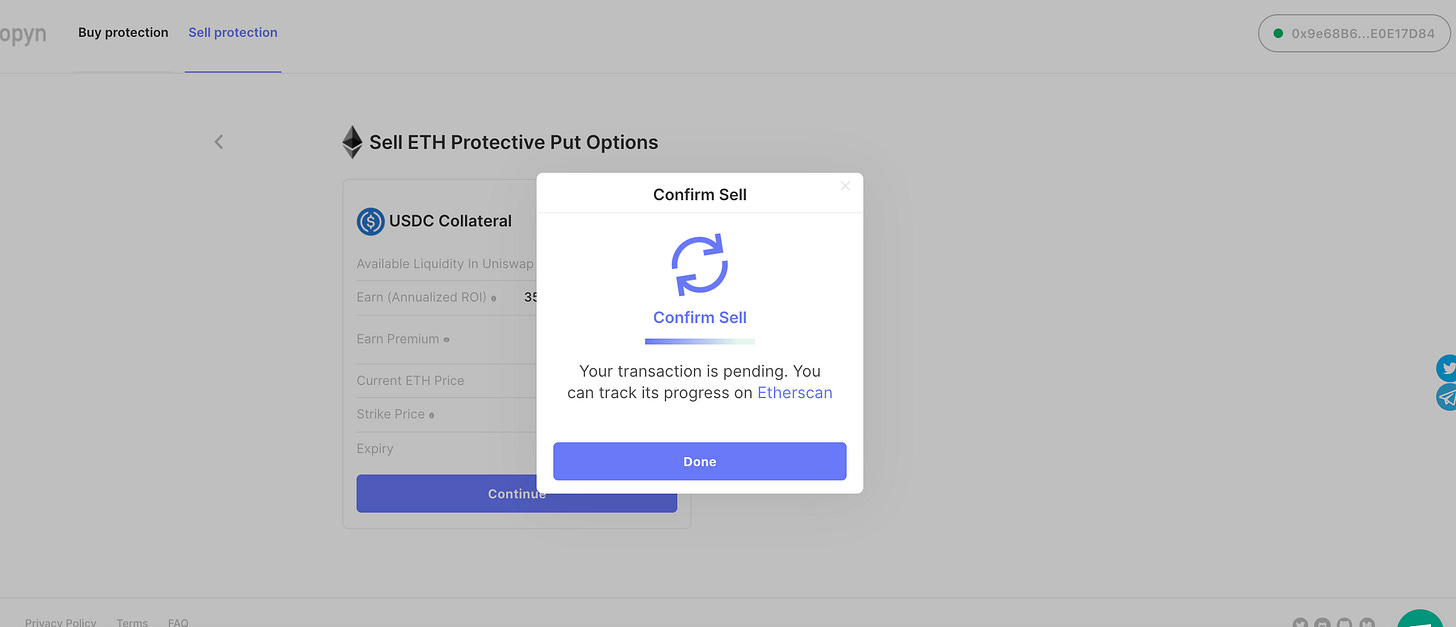
Click “confirm” and approve the transaction through MetaMask. Once that is done, you should see a screen like this

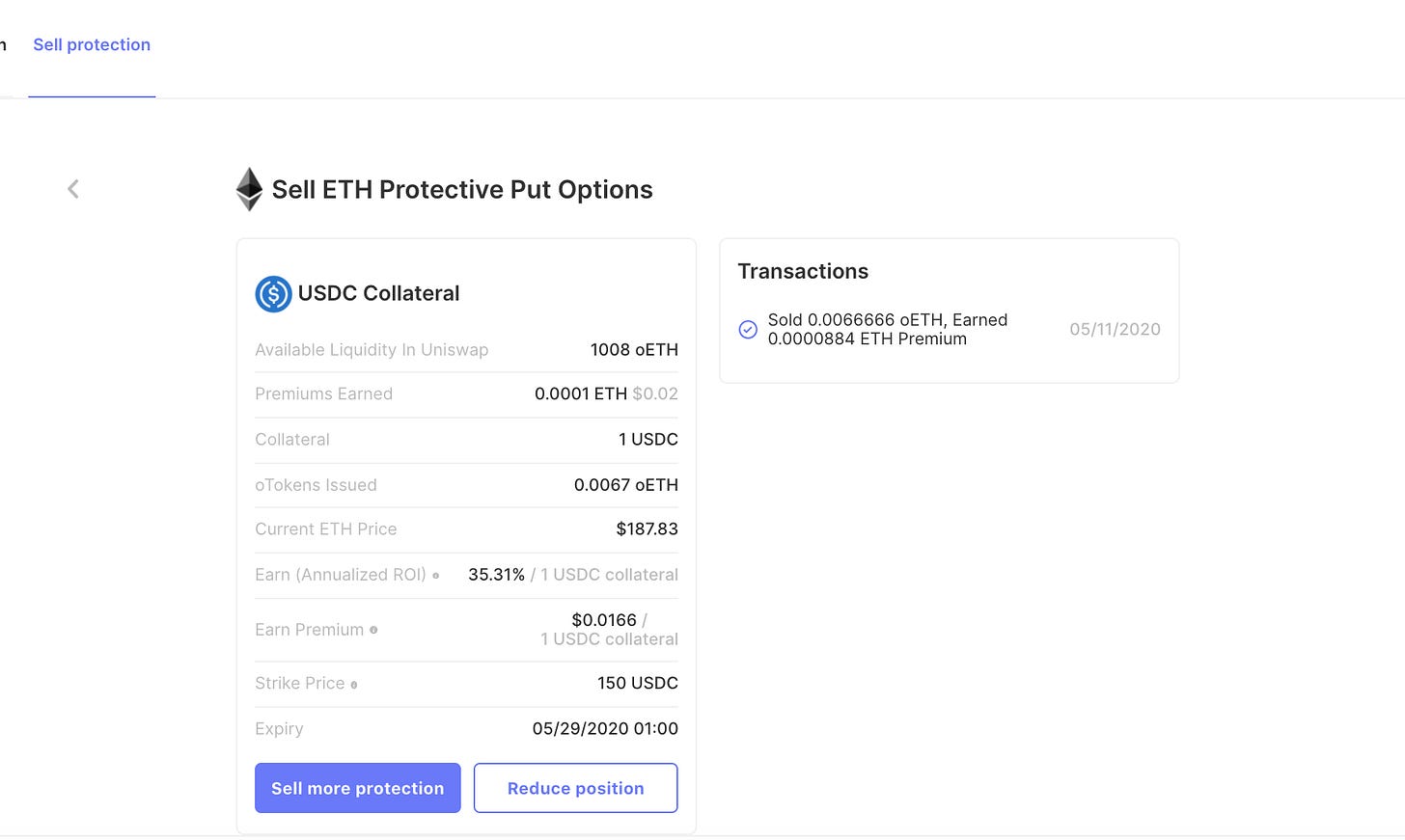
Once the transaction has been confirmed on Ethereum, you should be able to see your position on this page. Refresh the page to see the new view.

And that is it! You have earned a premium by selling a put option. You should see the ETH in your wallet.

What happens now?

If ETH falls below the strike price, you might get exercised on. In other words, someone might sell you their ETH for the USDC that you have locked in the vault.

Polymarket

Set Protocol

Synthetix

                Speculate on DeFi tokens with binary options

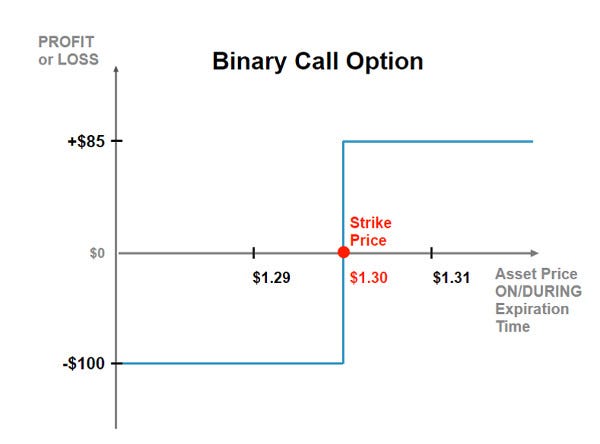
                How do binary options work?

Let’s consider two implementations of binary options in DeFi: Synthetix and Opium.

The Synthetix implementation of binary options is based on so-called “Pari-mutuel markets” (yes that’s the correct spelling), which means that the payout of winners to losers is determined by the relative capital pool size of longs and shorts.

Pari-Mutuel = Bet Together. This means all bets go into one pool so the price of any given contract reflects the opinions of market participants. In other words, you are competing against other participants, not the house.

Every binary options market on Synthetix has a “bidding phase” in which traders can place bids for long and short positions.

After a fixed time period, the bidding phase is closed and the payouts are fixed based on the spread between long and short bids. Traders can then either trade their positions on secondary markets or wait until maturity. At maturity, the winning traders can exercise their options for the previously determined payout. Traders can specify how much margin they want to lock upfront, however, their potential payoff is unknown until a later stage.

On Opium, binary options are implemented based on a fixed initial margin which means that the maximum payoff of losers to winners is known upfront and therefore risk is mitigated. Professional traders who use options to hedge their trading risks generally prefer this implementation of decentralized derivatives. Traders can get the desired price exposure through buying a certain volume of long or short contracts for the right price (eg. a trader buys 3 binary options contracts on Opium with $50 margin each to have a total of $150 invested).

In comparison, Synthetix currently offers more markets and guaranteed execution. Binary options on Opium are more predictable and therefore more suitable for traders that want to hedge risks, however, execution of trades is depending on liquidity.

Zerion